Een spreidingsdiagram wordt toegepast om de samenhang tussen twee (te onderzoeken) aspecten in kaart te brengen.
Tijdens correlatieonderzoeken is het spreidingsdiagram dan ook een veel gebruikte methodiek, teneinde:
- (deel-)processen te kunnen meten en begrijpen;
- mogelijke oorzaken te identificeren.
Het is belangrijk oorzaak en gevolg niet als twee afzonderlijke aspecten te zien, maar de relatie ertussen vast te kunnen stellen. Een spreidingsdiagram geeft in tegenstelling tot veel andere methodieken geen bewijs dat de ene situatie optreedt als gevolg van een andere situatie, maar toont daarentegen het onderlinge verband. Indien er min of meer een (lineaire) samenhang tussen 2 variabelen gedefinieerd kan worden, spreekt men van correlatie. Het kan hierbij dus gaan om de relatie tussen twee reeksen metingen, alsmede om de relatie tussen twee toevalsvariabelen.
Als gevolg van een vermoeden van samenhang tussen twee variabelen kan men besluiten een correlatieonderzoek uit te voeren. Hiermee kan worden aangetoond:
- of er daadwerkelijk correlatie bestaat tussen de variabelen;
- in welke mate er correlatie bestaat tussen de variabelen (correlatiecoëfficiënt);
- op welke wijze er correlatie bestaat tussen de variabelen.
Toepassing
Tijdens (kwaliteits-)verbeterprojecten wordt veelvuldig gebruik gemaakt van een spreidingsdiagram om in de diagnosefase van het traject de oorzaak-en-gevolgrelaties te definiëren. Indien er correlatie bestaat, kan de correlatiecoëfficiënt worden berekend.
De correlatiecoëfficiënt ligt altijd tussen 0 ± 1, waarbij:
- -1 = (volledig) negatieve correlatie;
- 0 = geen correlatie;
- 1 = (volledig) positieve correlatie.
Hoe dichter de correlatiecoëfficiënt bij de nulwaarde ligt, des te lager de correlatie.
Onderstaand worden 5 grafieken getoond, waarin verschillende correlaties zijn weergegeven. De regressielijn is hierbij ter illustratie grijs weergegeven (fictief).
Positieve correlatie
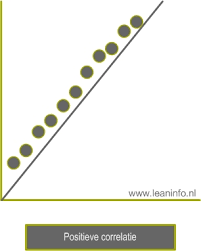
Matige positieve correlatie
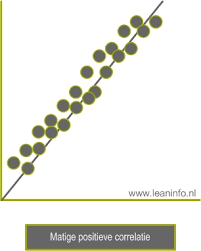
Slechte positieve correlatie
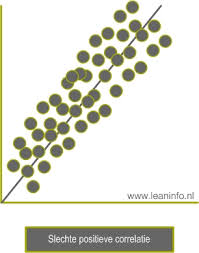
Geen correlatie

Negatieve correlatie

Het bepalen van positieve/negatieve correlatie kan het best worden uitgelegd met een voorbeeld:
- Positieve correlatie:
Medisch Instituut “MediX” doet onderzoek naar het verband tussen het lichaamsgewicht en de leeftijd van 12.350 proefpersonen in de leeftijdscategorie 21 – 56 jaar. Het onderzoek toont een relatie tussen de hoogte van het gemiddelde lichaamsgewicht en de gemiddelde leeftijd van de proefpersonen. Hieruit valt te concluderen dat de hoogte van het gemiddelde lichaamsgewicht stijgt wanneer de gemiddelde leeftijd van de proefpersonen toeneemt. Dit wordt positieve correlatie genoemd: een vermeerdering van de ene grootheid resulteert in een vermeerdering van de andere grootheid.
- Negatieve correlatie:
Medisch Instituut “MediX” doet eveneens onderzoek naar het verband tussen het lichaamsgewicht en de leeftijd van 5.600 proefpersonen in de leeftijdscategorie 68 – 84 jaar. Het tweede onderzoek toont eveneens een relatie tussen de hoogte van het gemiddelde lichaamsgewicht en de gemiddelde leeftijd van de proefpersonen; de hoogte van het gemiddelde lichaamsgewicht daalt wanneer de gemiddelde leeftijd van de proefpersonen toeneemt. Dit tweede verschijnsel wordt negatieve correlatie genoemd: een vermeerdering van de ene grootheid heeft een vermindering van de andere grootheid tot gevolg.
Terugkomend op de 3 aspecten uit een correlatieonderzoek kan met behulp van een spreidingsdiagram worden aangetoond of er sprake is van correlatie tussen de variabelen en op welke wijze er sprake is van correlatie (positief/negatief). De mate van correlatie kan vervolgens worden aangetoond met de correlatiecoëfficiënt.De correlatiecoëfficiënt is eenheidloos en wordt in de praktijk veelvuldig aangeduid met de letter R of ρ (rho). De coëfficiënt kan als volgt worden berekend:
R (x,y) = (Cov (x,y)) / (σ x * σ y), waarin:
- Cov(x,y) staat voor de covariantie van x en y;
- Covariantie is een maat voor de spreiding van 2 gekoppelde variabelen. De covariantie van x en y wordt in de statistiek aangeduid als Cov(x,y).
- σ x/y staat voor de standaarddeviatie van x/y.
- Standaarddeviatie is een maat voor de spreiding van een reeks getallen om het gemiddelde. De deviatie van bijvoorbeeld x wordt in de statistiek aangeduid als σ x. De standaarddeviatie staat eveneens bekend onder de naam standaardafwijking.
In de literatuur worden verschillende (veelvoorkomende) afgeleide behandeld, zoals:
= ( (∑ (xi – ẋ) (yi – ȳ)) / (√ (∑ (xi – ẋ)^2 (yi – ȳ))^2) )
In de voorbeelden is een duidelijke spreiding van de meetpunten weergegeven, verschillend in grootte. Hierdoor is het onmogelijk een rechte lijn te trekken welke door ieder meetpunt gaat. Aangezien de meetpunten wel bij benadering op één lijn liggen, kan het interessant zijn om de betreffende lijn te tekenen en zodoende het patroon van de meetpunten inzichtelijk te maken. Deze lijn wordt de regressielijn (-model) genoemd. In bijvoorbeeld grafiek 2 (‘Matige positieve correlatie’) is te zien dat de regressielijn, op een enkele na, door vrijwel geen van de meetpunten gaat. Dit betekent dat er meestal een afwijking optreedt tussen de ‘gemeten y-waarde’ en de ‘y-waarde van het regressiemodel’. De regressielijn wordt vervolgens getekend in de optimale (lees: ‘beste’) beschouwing, oftewel in de situatie waarin de som van alle gekwadrateerde afwijkingen het kleinst is. In de statistiek staat dit bekend onder de naam “kleinste-kwadratenmethode“. De regressielijn y = ax + b kan nu alsvolgt worden berekend:
- bepaal het gemiddelde van de x-waarden (= µ x);
- bepaal het gemiddelde van de gemeten y-waarden (= µ y);
- bepaal van alle x-waarden het gekwadrateerde verschil met µ x (= S xx);
- bepaal van alle y-waarden het product met de bijbehorende X-(µ x) en tel deze op (= S xy);
- bepaal de richtingscoëfficiënt van de regressielijn (= a);
- bepaal µ y – (a * µ x) (= b – startpunt).