Controlekaarten worden veelvuldig gebruikt ten behoeve van procesmonitoring. Hierbij wordt onder andere aandacht besteed aan de identificatie van variaties in verhouding tot de tijd.
Controlekaarten kunnen worden gebruikt om:
- (deel-)Processen te definiëren voor nader onderzoek
- Meten en begrijpen van (deel-)processen
- Vergelijken van de “before situation” en “after situation“
Binnen de statistische procesbeheersing (SPC) spelen controlekaarten een primaire rol bij het volgen en controleren van een proces. De controlekaart kan het best gezien worden als een lijndiagram voor procesgegevens, waarin statistisch bepaalde controlelijnen zijn gedefinieerd. Uitgezet tegen een tijdsperiode (bijv. een maand) kunnen er op een controlekaart gegevens worden verzameld welke een weergave bieden van het voortgangsproces. Afhankelijk van de categorie waarop een controlekaart wordt ingezet kunnen gegevens zodoende genoteerd worden. Bijvoorbeeld in de categorie “productie” kan worden vastgelegd hoe hoog de productie was. Hetzelfde geldt voor de hoeveelheid verstoringen binnen een proces in de categorie “storingen“.
De statistisch bepaalde controlelijnen zijn kenmerkend voor het beeld (de curve) van een controlekaart. Afwijkingen hierop (trendbreuk) kunnen door het gebruik van deze ‘regelgrenzen’ direct geïdentificeerd worden. Dit wijst vervolgens op problemen binnen het proces.
Op een controlekaart komen minimaal 3 regelgrenzen voor:
- LCL – Lower Control Limit: de ondergrens
- CL – Control Limit: nominaal
- UPL – Upper Control Limit: de bovengrens
Waardes binnen de regelgrenzen kunnen door de gebruiker(s) als normaal worden beschouwd. Bij overschrijding van de grenzen is er sprake van een zogeheten out-of-control situatie en dient men direct te anticiperen middels een onderzoek naar de afwijking.
Let op! Regelgrenzen mogen niet verward worden met specificaties of doelstellingen van het betreffende proces. Voor veel controlekaarten geldt dat de regelgrenzen gedefinieerd worden als zijnde ongeveer 2 à 3 maal de standaardafwijking van het gemiddelde (CL). Dit is echter afhankelijk van het type controlekaart dat gebruikt wordt. Aan iedere controlekaart zijn voorwaarden verbonden waaraan de gebruiker moet voldoen om het instrument op een verantwoorde wijze toe te passen teneinde het proces te meten. Dit betekent dat er ook per controlekaart andere formules gehanteerd worden om de regelgrenzen te berekenen. De standaarddeviatie, een begrip in de statistiek, speelt vanuit het oogpunt ‘spreiding’ hierbij een rol.
Het vinden van een compromis tussen krappe regelgrenzen en ruime regelgrenzen vormt de uitdaging. Een krappe regelgrens is bijvoorbeeld [ CL ± 1 S ], waarin S staat voor de standaarddeviatie. Krappe regelgrenzen hebben veel loos alarm tot gevolg, waardoor betrokkenen op den duur minder alert worden. Andersom leiden ruime regelgrenzen voor (te) late signalering van problemen.
Gegevens
Het type controlekaart is onder andere afhankelijk van het soort gegevens. In het algemeen wordt er onderscheidt gemaakt tussen Discrete variabelen en Continue variabelen.
Van een discrete variabelen kunnen slechts bepaalde waarden voorkomen, bijvoorbeeld alleen gehele getallen. Discrete gegevens kunnen worden geteld en hebben betrekking op attributieve proceseigenschappen. Oftewel, waarmee één enkele kwalitatieve eigenschap van het beschouwde object wordt aangegeven.
Voor continue variabelen geldt dat er tussen twee gegeven waarden altijd een andere ligt. Continue gegevens zijn meetbaar en hebben dan ook betrekking op variabele eigenschappen.
P-kaarten, C-kaarten, NP-kaarten en U-kaarten zijn type controlekaarten welke gebruikt kunnen worden in het geval van discrete gegevens. Een ẋR-kaart is een type controlekaart voor continue gegevens.
Toepassing
Het toepassen van controlekaarten vergt enige mate van kennis met betrekking tot de achtergrond van de methodiek. Het (correct) interpreteren van controlekaarten is echter het punt waar niet alleen nieuwe gebruikers, maar ook veel (startende) beoefenaren moeite mee hebben. Controlekaarten worden gemaakt om een proces te monitoren en te bepalen of een proces statistisch beheerst is of niet. De wijze waarop een controlekaart wordt geïnterpreteerd is voor de betrouwbaarheid van dit oordeel dan ook zeer belangrijk!
In de literatuur worden tal van richtlijnen behandeld welke een indicatie geven waarop controlekaarten kunnen worden verwerkt. Primair kunnen we spreken van een out-of-control situatie, wanneer:
- één of meerdere punten buiten de regelgrenzen (LSL – USL) vallen
- minimaal tien meetpunten achter elkaar onder of boven nominaal (CL)
- minimaal zes meetpunten achter elkaar een stijgende of dalende trend (lijn)
Naast deze eenvoudig toe te passen ‘zwart-wit’ richtlijnen wordt er tijdens de beoordeling van controlekaarten ook een beroep gedaan op het inzicht en analytisch vermogen van de gebruiker, om de ‘grijze’ gebieden eveneens correct te interpreteren. Wanneer bijvoorbeeld aan het eind van een controlekaart een vijftal dalende meetpunten worden gedefinieerd, of er sprake is van een instabiele trend door bijvoorbeeld veel afwisseling in stijgende en dalende karakters (binnen de grenzen), kan het noodzakelijk zijn het proces aandachtig aan een onderzoek te onderwerpen. Dergelijke situaties kunnen voor komen, terwijl bovenstaande out-of-control aspecten niet worden geregistreerd. Belangrijk is dat men nooit een proces wijzigt/verbetert gedurende een meting. Dit maakt het gebruik van de controlekaart waardeloos! Rond de meting altijd eerst volledig af.
In onderstaand voorbeeld zal een ẋR-kaart worden behandeld.
Een ẋR-kaart bestaat uit 2 kaarten:
- De ẋ-kaart is volledig gebaseerd op het gemiddelde
- De R-kaart behandelt de Range, oftewel de spreiding
Naast de ẋR-kaart wordt eveneens veel gebruik gemaakt van de Me/R-kaart, waarin ‘Me’ staat voor Mediaan. Let op! Gemiddelde en Mediaan zijn niet hetzelfde!
- Gemiddelde: de som van de getallen gedeeld door het aantal getallen. Voorbeeld: reeks (1,4,1,6,5,3,3,1,2) ; gemiddelde = 2,88.
- Mediaan: het middelste getal van een reeks, nadat deze van klein naar groot zijn gesorteerd. In het geval van een reeks van ‘n’ getallen, waarin ‘n’ is een even getal, is er geen middelste getal. In dit geval is de mediaan het gemiddelde van de twee middelste getallen. Voorbeeld: reeks (1,1,1,2,3,3,4,5,6) ; mediaan = 3.
Voorbeeld
Firma “Tire-X” is marktleider op het gebied van de productie van automobiel- en truckbanden. Door een recessie hebben veel (ervaren) medewerkers hun baan verloren en zijn er goedkopere arbeidskrachten met een tijdelijk contract aangenomen. Eén van de mogelijke gevolgen hiervan is een afnemende productkwaliteit, doordat veel proceskennis verloren is gegaan. Het bedrijf besluit een aantal kritische processen te monitoren met behulp van controlekaarten, teneinde een conclusie te kunnen trekken of het proces zich volgens de proces-eigen variatie gedraagt.
Een kwalitatief goede band bestaat onder andere uit een aantal belangrijke grondstoffen in de juiste verhoudingen. Grondstof ‘Y’ is een belangrijk hechtingsmiddel en dient in de juiste hoeveelheid aan het product te worden toegevoegd. Teveel mg van grondstof ‘Y’ kan ervoor zorgen dat de band onvoldoende uithard, terwijl een te lage hoeveelheid ervoor zorgt dat het karkas niet aan het rubber hecht. Het toevoegen van grondstof ‘Y’ aan het product is dan ook één van de processen met een sterke focus op nauwkeurigheid, doch zeer beïnvloedbaar door manafhankelijke disciplines.
De leidinggevende van de afdeling ‘Raw Materials’ besluit om een meting (steekproef) uit te voeren op tien producten. Hiervoor wordt gebruik gemaakt van een ẋR-kaart, aangezien men te maken heeft met continue gegevens. Onderstaand zijn de resultaten weergegeven. Hierbij geldt dat de Range wordt bepaald door het verschil tussen de grootste en de kleinste meetwaarde in de steekproef.
| Steekproef – n | Gemiddelde – ẋ | Range – R |
| 01 | 17,2 | 2,1 |
| 02 | 17,1 | 2,3 |
| 03 | 16,4 | 1,9 |
| 04 | 16,9 | 2,2 |
| 05 | 16,6 | 1,7 |
| 06 | 16,7 | 1,6 |
| 07 | 17,1 | 1,8 |
| 08 | 16,8 | 1,6 |
| 09 | 16,7 | 2,2 |
| 10 | 16,6 | 1,8 |
- ẍ = (∑ẋ) / n = 16,8
- Ṙ = (∑R) / n = 1,9
Waarbij:
- ẍ : het gemiddelde van de gemiddelde waarnemingen uit elke steekproef
- Ṙ : het gemiddelde van de Ranges
Nadat de steekproeven zijn uitgevoerd wordt er gestart met het berekenen van de regelgrenzen voor zowel de ẋ-kaart alsmede de R-kaart.
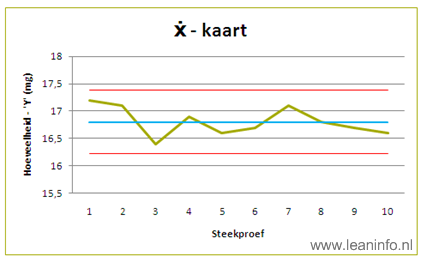
ẋ-kaart
Voor het berekenen van de regelgrenzen van de ẋ-kaart worden onderstaande formules gebruikt.
- UCL – ẋ = ẍ + (A2 * Ṙ)
- UCL – ẋ = 16,8 + (0,308 * 1,9) = 17,39
- CL – ẋ = ẍ
- CL – ẋ = 16,8
- LCL – ẋ = ẍ – (A2 * Ṙ)
- LCL – ẋ = 16,8 – (0,308 * 1,9) = 16,21
Waarbij:
- A2: een constante die afhankelijk is van het aantal uitgevoerde steekproeven. Zie tabel A
R-kaart
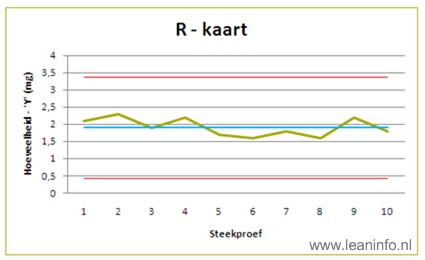
Voor het berekenen van de regelgrenzen van de R-kaart worden onderstaande formules gebruikt.
- UCL – R = (D4 * Ṙ)
- UCL – R = 1,777 * 1,9 = 3,38
- CL – R = Ṙ
- CL – R = 1,9
- LCL – R = (D3 * Ṙ)
- LCL – R = 0,223 * 1,9 = 0,42
Waarbij:
- D3/D4: constanten die afhankelijk zijn van het aantal steekproeven. Zie tabel A.
Tabel A– Constanten voor het bepalen van regelgrenzen in steekproecen zonder structuur en zonder extra tussen-streekproefvariatie.
| Steekproef – n | Regekaart – ẋ | Regelkaart – R | |
| A2 | D3 | D4 | |
| 2 | 1,880 | 0 | 3,267 |
| 3 | 1,023 | 0 | 2,575 |
| 4 | 0,729 | 0 | 2,282 |
| 5 | 0,577 | 0 | 2,115 |
| 6 | 0,483 | 0 | 2,004 |
| 7 | 0,419 | 0,076 | 1,924 |
| 8 | 0,373 | 0,136 | 1,864 |
| 9 | 0,337 | 0,184 | 1,816 |
| 10 | 0,308 | 0,223 | 1,777 |
Interpretatie
Beide kaarten worden door de firma ‘Tire-X’ afzonderlijk geïnterpreteerd.
Allereerst kan er gesteld worden dat de ẋ-kaart statistisch beheerst is. Deze conclusie kan worden getrokken wanneer het resultaat wordt vergeleken met de eerder genoemde criteria:
- één of meerdere punten buiten de regelgrenzen (LSL – USL) vallen; NEE
- minimaal tien meetpunten achtereenvolgens onder of boven nominaal (CL); NEE
- minimaal zes meetpunten achtereenvolgens een stijgende of dalende trend (lijn). NEE
De R-kaart kan eveneens als statistisch beheerst worden bestempeld. De mate van variatie in deze kaart is lager dan bij de ẋ-kaart en bovenstaande criteria zijn niet van toepassing.
Bovenstaand fictief voorbeeld toont aan hoe een firma gebruik kan maken van controlekaarten (ẋR-kaarten). Het resultaat geeft een goed beeld waaruit geconcludeerd kan worden dat men hier te maken heeft met een gecontroleerde (beheerst) procesafloop, oftewel: zonder veel fluctuatie in spreiding en ligging. Het bijsturen van (bij meermalige benadering van de regelgrenzen) of drastische ingrijpen in (bij overschrijding van de regelgrenzen) het proces zijn niet noodzakelijk.